付注1-4-1 構造方程式モデリングについて
第1部第4章第1節における構造方程式モデリングを用いた分析方法について、補足を行う。
構造方程式モデリング(SEM:Structural Equation Modeling)とは、仮説として設定した多数の変数間の関係を、線形結合の形にモデリングして行う分析をいう。仮説の妥当性を検証する際に、特に有用な分析手法である。構造方程式モデリングでは、相関分析、回帰分析、因子分析を統合した分析が可能であり、メリットとして、潜在変数と呼ばれる直接は観測できない因子を含めての分析を行える点や、一つの分析内で複数の従属変数を設定できる点が挙げられる。
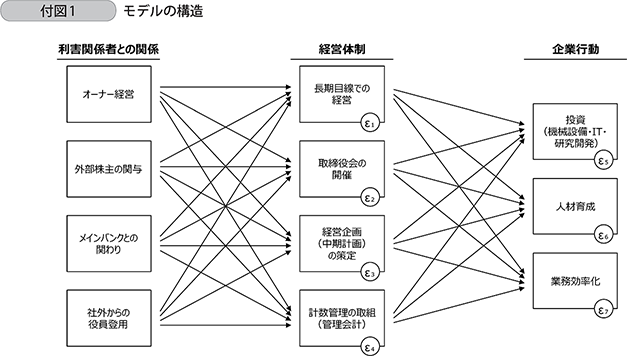
今回の分析では、各観測変数を「利害関係者との関係」、「経営体制」、及び「企業行動」に分類し、「利害関係者との関係」に属する指標群から「経営体制」に属する指標群へ、「経営体制」に属する指標群から「企業行動」に属する指標群へ、それぞれパスをひいた分析モデルを設定した。なお、本分析において潜在変数は設定していない。
また、各指標は0もしくは1を取るダミー変数であるため、各変数間のパスはプロビット法によってモデリングした。よって、プロビット回帰モデルに対応する一般化構造方程式モデリング(GSEM:Generalized Structural Equation Modeling)を採用している。
なお、「経営体制」と「企業行動」に属する指標群に重ねて配置したαiはそれぞれ定数項の係数を示す。
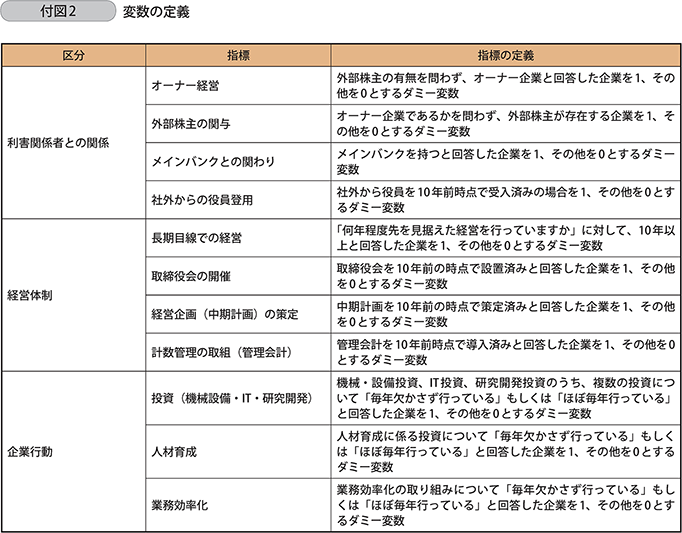
各指標はいずれも、2017年11月に中小企業等10,000社を対象にしたアンケート調査(回収率24.2%)により取得した情報を用いた。使用した変数は以下の通り。
推定結果は以下の通り。